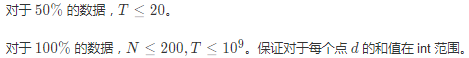题目描述
输入格式
输出格式
数据范围
样例输入
3 20 1 00 1 41 0 24 2 0样例输出
0.4000000.3500000.250000题目来源
本题是一道概率DP,并且很容易模拟出过程。
先预处理出两两点之间的最短路,本题可以用O(n3)的算法。
两个点之间的传递概率可以预处理,也可以记忆化处理,这里给一份记忆化计算从i点到j点的概率的代码
inline double calc(int i,int j){ if(gl[i][j]!=0) return gl[i][j]; int res=0; for (register int k=1;k<=n;++k) res+=mp[i][k]; return gl[i][j]=(double)((double)mp[i][j]/(double)res);} 同时我们可以注意到(测试出),当T大到一定值的时候,答案的大小就基本恒定不变了(差异<0.0000001,符合题目要求),也就是说当T的值很大的时候,各点的概率趋近平衡,在1e-6的精度要求下,从数值上看是不变的了。
那么我们就可以不用在意Tmax=1e9了,我们在读入T之后加上 T=min(T,4000) 即可。当然,这里的4000不是特定的,如果您有更合适的值也可以。4000是可以AC本题的。(我们也可以不限制T,转而维护一个eps:若最近两次更新到某点的概率的差值<1e-7,我们就结束推导过程)
同时本题直接开数组是开不下的,我们注意到当前状态仅由上一次的推导而来(对应题目中“在传递到下一个节点后,该数据包会自动删除在当前节点的备份。”这句话)。
所以我们可以加上滚动数组的优化,当前状态由上一状态的所有点的概率乘以传递概率求和而来。最后输出结果即可
附上AC代码


1 #include2 #include 3 #include 4 using namespace std; 5 template inline void read(_T &_a) 6 { 7 char _ch=getchar();_a=0; 8 while(_ch<'0'||_ch>'9')_ch=getchar(); 9 while(_ch>='0'&&_ch<='9'){_a=(_a<<3)+(_a<<1)+_ch-'0';_ch=getchar();}10 }11 12 const int maxn=201,maxm=19901;13 int n,T,mp[maxn][maxn];14 double dp[2][maxn],gl[maxn][maxn];15 bool flag;16 17 inline double calc(int i,int j)18 {19 if(gl[i][j]!=0) return gl[i][j];20 int res=0;21 for (register int k=1;k<=n;++k) res+=mp[i][k];22 return gl[i][j]=(double)((double)mp[i][j]/(double)res);23 }24 25 int main()26 {27 freopen("trans.in","r",stdin);28 freopen("trans.out","w",stdout);29 read(n); read(T);30 memset(mp,0x7f,sizeof(mp));31 for (register int i=1;i<=n;++i) scanf("%lf",&dp[1][i]);32 for (register int i=1;i<=n;++i)33 for (register int v=1;v<=n;++v)34 read(mp[i][v]),mp[v][i]=mp[i][v];35 for (register int k=1;k<=n;++k)36 for (register int i=1;i<=n;++i)37 for (register int j=1;j<=n;++j)38 mp[i][j]=min(mp[i][j],mp[i][k]+mp[k][j]);39 T=min(T,4000);40 while(T--)41 {42 bool nxt=flag^1;43 for (register int i=1;i<=n;++i)44 {45 dp[flag][i]=0;46 for (register int v=1;v<=n;++v)47 if(i!=v) dp[flag][i]+=dp[nxt][v]*calc(v,i);48 }49 flag=nxt;50 }51 flag^=1;52 for (register int i=1;i<=n;++i) printf("%lf\n",dp[flag][i]);53 return 0;54 }